CUMTOJ数据结构实验考试

数据结构 C++ 数据结构

发布时间 : 2019-10-23 20:51

阅读 :

问题 A: 求素数

题目描述

求0 ~ N内的素数。(N<=100000)

输入

输出

[0～N]之间的所有素数，一个素数占一行。

样例输入

100

样例输出

2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97

代码

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <stdlib.h>
#include <string.h>
#include <math.h>
using namespace std;
int N;
int main()
{
	bool isSuShu(int num);
	int i;
	cin >> N;
	for(i = 2; i <= N; i++)
	{
		if(isSuShu(i))
		{
			cout << i << endl;
		}
	}
	return 0;
}
bool isSuShu(int num)
{
	int tmp = sqrt(num);
	int i, j;
	for(i = 2; i <= tmp; i++)
	{
		if(num % i == 0)
		{
			return false;
		}
	}
	return true;
}

问题 B: 水仙花数

题目描述

春天是鲜花的季节，水仙花就是其中最迷人的代表，数学上有个水仙花数，他是这样定义的：
“水仙花数”是指一个三位数，它的各位数字的立方和等于其本身，比如：153=1^3+5^3+3^3。
现在要求输出所有在m和n范围内的水仙花数。

输入

两个整数m和n（100<=m<=n<=999）。

输出

要求输出所有在给定范围内的水仙花数，就是说，输出的水仙花数必须大于等于m,并且小于等于n，如果有多个，则要求从小到大排列在一行内输出，之间用一个空格隔开;
如果给定的范围内不存在水仙花数，则输出no。

样例输入

300 380

样例输出

370 371

代码

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <stdlib.h>
#include <string.h>
#include <math.h>
using namespace std;
int main()
{
	bool isShuiXian(int num);
	int i, flag = 0;
	int m, n;
	cin >> m;
	cin >> n;
	for(i = m; i <= n; i++)
	{
		if(isShuiXian(i))
		{
			cout << i << " ";
			flag++;
		}
	}
	if(flag)
		cout << endl;
	else
		cout << "no" << endl;
	return 0;
}
bool isShuiXian(int num)
{
	int bai, shi, ge;
	bai = num / 100;
	shi = (num - bai * 100) / 10;
	ge = num - bai * 100 - shi * 10;
	if(num == (bai * bai * bai + shi * shi * shi + ge * ge * ge))
		return true;
	else 
		return false;
}

问题 C: 汽水瓶【25】

题目描述

有这样一道智力题：“某商店规定：三个空汽水瓶可以换一瓶汽水。小张手上有十个空汽水瓶，她最多可以换多少瓶汽水喝？”答案是5瓶，方法如下：先用9个空瓶子换3瓶汽水，喝掉3瓶满的，喝完以后4个空瓶子，用3个再换一瓶，喝掉这瓶满的，这时候剩2个空瓶子。然后你让老板先借给你一瓶汽水，喝掉这瓶满的，喝完以后用3个空瓶子换一瓶满的还给老板。如果小张手上有n个空汽水瓶，最多可以换多少瓶汽水喝？

输入

输入文件最多包含10组测试数据，每个数据占一行，仅包含一个正整数n(1≤n≤100)，表示小张手上的空汽水瓶数。n=0表示输入结束，你的程序不应当处理这一行。

输出

对于每组测试数据，输出一行，表示最多可以喝的汽水瓶数。如果一瓶也喝不到，输出 0

样例输入

3
10
81
0

样例输出

1
5
40

代码

思路1

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <stdlib.h>
#include <string.h>
#include <math.h>
using namespace std;
int main()
{
    int n;
    while(cin >> n)
	{
		if(n)
		{
			int result = 0 , emp = n , tmp;
			while(emp >= 2)
			{
				if(emp == 2)
					emp++;
				tmp = emp / 3;
				result += tmp;
				emp = emp % 3 + tmp;
			}
			cout << result<< endl;
		}
		else
			break;
    }
    return 0;
}

思路2（神坑思路，啥都别管，直接除于2）

#include <iostream>
using namespace std;
int main()
{
	int num;
	while(cin >> num && num)
	{
		cout << num / 2 << endl;
	}
	return 0;
}

问题 D: 数列【15】

题目描述

小明今天在做数学题的时候碰到这样一个问题，一个数列的定义如下：
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7。
现在给你A,B和n的值，请问你f(n)的值是多少？

输入

输入包含多组测试数据。
每组输入3个整数A,B和n（1<=A,B<=1000，1<=n<=100000000），当输入的3个数都为0时，输入结束。

输出

对于每组输入，输出f(n)的值。

样例输入

1 1 3
1 2 10
0 0 0

样例输出

2
5

代码

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <stdlib.h>
#include <string.h>
#include <math.h>
using namespace std;
int A, B;
int main()
{
	int f(int num);
	int N;
	while((cin >> A , cin >> B , cin >> N))
	{
		if(A && B && N)
			cout << f(N) << endl;
		else
			break;
	}
	return 0;
}
int f(int num)
{
	if(num == 1)
		return 1;
	if(num == 2)
		return 1;
	//f(num) = (A * f(num - 1) + B * f(num - 2)) mod 7;
	if(num > 2)
		return (A * f(num - 1) + B * f(num - 2)) % 7;
}

问题 E: 算法9-5 ~ 9-8：二叉排序树的基本操作

题目描述

二叉排序树或者是一棵空树，或者是具有以下几条性质的二叉树：

1 若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值；
2 若它的右子树不空，则右子树上所有结点的值均大于它的根节点的值；
3 它的左右子树也分别为二叉排序树。

二叉排序树又可以被称为二叉查找树，根据上述定义的结构不难知道，它的查找过程十分简单，只需要通过不断的将当前结点的值与需要查找的值进行比较，如果相等则直接输出，如果要查找的值更小则深入至左子树进行比较，否则就深入右子树进行比较，直到找到相应的值或者进入了一棵不存在的子树为止。
其查找过程可以描述如下：

而其插入过程同样也十分简洁，可以描述如下：

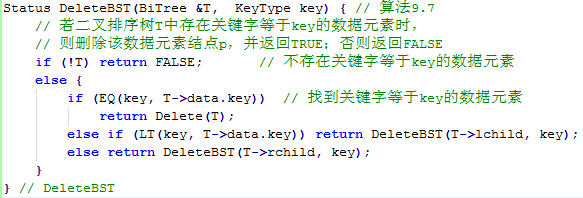
而删除操作可以描述为如下的两个算法：

在本题中，读入一串整数，首先利用这些整数构造一棵二叉排序树。另外给定多次查询，利用构造出的二叉排序树，判断每一次查询是否成功。

输入

输入的第一行包含2个正整数n和k，分别表示共有n个整数和k次查询。其中n不超过500，k同样不超过500。
第二行包含n个用空格隔开的正整数，表示n个整数。
第三行包含k个用空格隔开的正整数，表示k次查询的目标。

输出

只有1行，包含k个整数，分别表示每一次的查询结果。如果在查询中找到了对应的整数，则输出1，否则输出0。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入

8 3
1 3 5 7 8 9 10 15
9 2 5

样例输出

1 0 1

提示

在本题中，首先需要按照题目描述中的算法完成二叉排序树的构造过程，之后需要通过在二叉排序树中的不断向下查找，将需要查询的值与当前节点的值进行比较，直到确定被查询的值是否存在。

通过课本中的性能分析部分，不难发现二叉排序树的平均查找长度是和logn同数量级的，但是，在某些特殊情况下二叉排序树将会退化，使查找的效率大大降低，这时就需要引入二叉排序树的平衡操作，利用平衡二叉树来保证查找的效率始终维持在logn的数量级上。

代码

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <iostream>
using namespace std;
const int max_num = 1000;
struct node
{
	int data;
	node *left, *right;
};
void insert(node* &root , int x)
{
	if(root == NULL)
	{
		root = new node;
		root->data = x;
		root->left = root->right = NULL;
	}
	else if(x == root->data) 
		return;
	else if(x < root->data)
		insert(root->left, x);
	else
		insert(root->right, x);
}
bool preorder(node* root, int num)
{
	if(root == NULL)
	{
		return false;
	}
	if(root -> data == num)
	{
		return true;
	}
	preorder(root->left, num);
	preorder(root->right, num);
}
int main()
{
	int n, k, x, i;
	int arr[max_num] = { 0 };
	memset(arr, -1, 4000);
	cin >> n >> k;
	node *root = NULL;
	for(i = 0; i < n; i++)
	{
		cin >> x;
		insert(root, x);
	}
	for(i = 0; i < k; i++)
	{
		cin >> arr[i];
	}
	for(i = 0; i < k; i++)
	{
		if(preorder(root, arr[i]))
			cout << "1" << " ";
		else
			cout << "0" << " ";
	}
	cout << endl;
	return 0;
}

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，可以邮件至 xingshuaikun@163.com。