二分法求方程的根

Cpp C++ 算法

发布时间 : 2019-10-23 17:50

阅读 :

1 算法思想
2 示例
1. 2.1 代码
2. 2.3 输出结果

1 算法思想

首先确定有根区间，将区间二等分，通过判断f（x）的符号，逐步将有根区间缩小，直至有根区间足够小，便可求出满足精度要求的近似值。

流程图如下

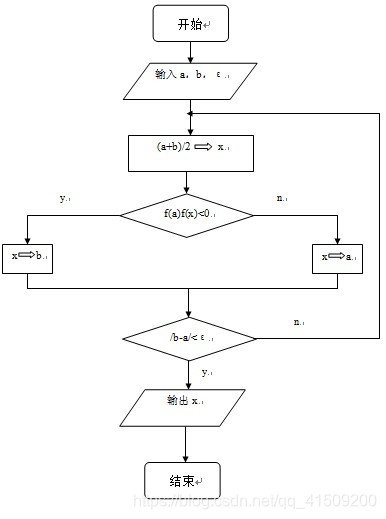
二分法求方程的根

2 示例

2.1 代码

#include <iostream>
#include <math.h>
using namespace std;
int main()
{
	float exp(float x);
    float left, right, accuracy, mid;
	cout << "请输入区间左端点值、右端点值和精确度：" << endl;
    cin >> left >> right >> accuracy;
    while(fabs(right - left) >= accuracy)
    {
        mid = (left + right) / 2;
        if(exp(left) * exp(mid) < 0)
        {
            right = mid;
        }
        else
        {
            left = mid;
        }
    }
    cout << "满足要求的值是：" << mid << endl;
    return 0;
}
float exp(float x)
{
    return x * x * x - x - 1;
}

2.3 输出结果

二分法求方程的解

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，可以邮件至 xingshuaikun@163.com。